機能創造理工学II <<<戻る
2009年 担当、後藤貴行
|
何を学ぶか |
これまで学んだニュートン運動方程式を使えば、微分方程式(=数学)さえ出来れば、ロボットでもスペースシャトルでも回転寿司の回る台でも、日常におけるすべての運動の問題が解けます。しかし、現代社会においてニュートン力学を適用出来ないケースが三つ存在します。それは、
の場合です。現代社会を支える、金属、半導体の中の電子は1と2にあてはまりますし、光通信やレーザーに登場する光子は3です。光を操作したり検知するデバイスを作るには1-3の全てが必要です。それから、未だに殆ど解明されていない現象の代表例として、摩擦があります。表面がつるつるしていれば良いかと言うとそうではなく、原子レベルで平坦な金属を貼り合わせると滑るどころかくっついて離れません。これを理解するのにも1と2が必要です。実は、1と2を理解するための科目は、「統計力学」と、「量子力学」と言って、これから先、どんどん習って行くわけですが、その準備をするための講義が機能創造理工学IIです。
※ 3は「相対論」です。残念ながら、本講義では深く取り扱うことはしません。
|
講義ノート |

試験の過去問(解析力学という科目をwebページ内で検索して、その試験問題を見て下さい)
大学院入試にもいくつか、解析力学から出題されています。
|
試験結果 |
問題が易しすぎたのでしょうか、満点が続出しました。但し、かなり甘く採点してあります。
例えば、問1でラグランジアンの重力ポテンシャルの符号を逆にしている人は半数以上いましたが、それは「z軸の方向を逆にとった」と好意的に解釈し、問5のハミルトニアンの式とコンシステントであれば加点してあります。また、問3で、調和振動子の運動方程式を解けない人も半数以上いましたが、これも、微分方程式を導けただけで正答としました。
それから、最後の断熱不変量の問題は、ざっと2lp0を評価すると確かに微小量の二次だけが残るのですが、まじめに、周期運動からのずれを計算してしまうと、微小量の一次の項が残ってしまいます(極めてゆっくりな変化であるとして、無視します)。混乱させたお詫びに、計算途中まで書いてあれば正答としました。講義終了後も質問があればどうぞ。
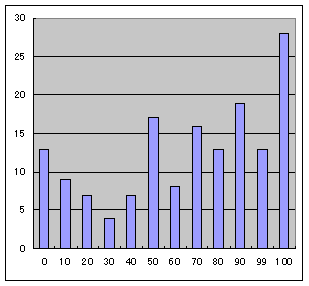
(横軸の100は満点、99は90点台、以下同様)