当日の講義予定内容や計算を、およそ10ページ程度にまとめたものです。
統計力学の担当は今年度初めてですので、大体、1〜2週間かけて準備
します。これを公開することも考えたのですが、講義はしっかり手でメモを
取る(これは講義だけでなく、将来、学会や研究会などに出たときも同様)
習慣をつけて欲しいのと、特に初版はタイプミスがかなりあるので、今の
ところ一般公開は予定していません。
代わりと言っては何ですが、講義担当が今年度で終了した解析力学につ
いて、最終版のノートを限定公開しておきます。 ノートの例(解析力学/pdf)
はて、統計力学では出てこないと思いますが、「直積」を表すのに良く使われ
ますね。たとえば、三次元のベクトルは、一次元座標三つの直積です。
N=Si <ni>= 1/[exp(b (0-m))-1] +6/[exp(b (e1-m))-1] +12/[exp(b (e2-m))-1]+...
に出てくる6とか12はどこから出るの? <<<TOP
大変良い質問なのでレポートNo.3にしました。
大きいのは意外な感じがしました。 <<<TOP
そうでしょう。ほんとに不思議ですね。このパウリ排他律による斥力は
中性子星や白色矮星など、超高密度の星が重力に耐えている源にも
なっています。
大きな階段教室での講義をイメージして下さい。静かな状態(≡絶対零度)では、
前方の低い位置の座席から順番に埋まって行き、最後の人(一番エネルギーが高い)
が座った位置がフェルミ波数です。
念のため、Fermiエネルギー、Fermi波数、Fermi波長、Fermi温度、Fermi速度などは
全て、単に単位を変えて表しただけのものです。
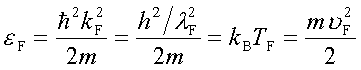
教室が、騒がしくなると(≡高温)、必ずしも、最前列から埋まるのではなく、
とびとびに間を空けて着席したり、わざわざ、後ろの席に座ったりします。
ボソンは、一つの椅子に何人も座れますから、Fermi波数に対応するような
ものはありません。但し、絶対零度での最大波数という定義を強いて
使うのであれば、絶対零度では全粒子がボースアインシュタイン凝縮して
いますから、Bose波数=0 です。
もしスピンが無ければ、一つの波数ベクトルを指定すると一つの状態が決まります。
もし、スピンSがあれば、一つの波数ベクトルを指定すると、2S+1個の状態が
対応します。
ちなみに、一つのエネルギーを指定すると、そのエネルギーでの「状態密度」個の
状態が決まります。
Bosonのときは、どうしてexp(-b(e-m)) <<1と言えるのですか? <<<TOP
ボソンの場合、m<0なので、基底状態のエネルギーをe=0ととれば、常に
exp(-b(e-m)) <1です。
もし、<<1 にこだわるのであれば、数学を復習してみてください。上記の
展開式の収束条件は、| x |<1です。
途中の項で和を止めても大体良い近似であるという条件が| x |<<1です。
現実の世界ではどういう現象なのですか? <<<TOP
固体の場合に限定しますと、
1)古典統計が使えるのは、
内殻の局在電子(1s,2s,2p...)、4f 軌道の電子、そして、He以外の原子核
などです。
2)古典統計が使えないのは、
最外殻のs電子など(これが自由電子)
He(3He, 4He)の原子核 (軽いので、極低温下で加圧して固化させても、
零点振動のために、意外と動き回る)
などです。なお、
格子振動やスピンの動きを粒子として捉えた現象(マグノンやフォノン)
も、固体内で動き回りますから、量子統計で扱う必要があります。
3)微妙なのは、
3d軌道の電子です。これは、遍歴電子とも呼ばれ、それほど自由でもなく、
といって、局在しているわけでもなく、固体の中を動き回っています。
なお、「どの統計を使うべきか」、ということ自体が大問題です。詳しくは、
固体物理I、II、実験学(磁気共鳴)、実験学(低温) などの講義で。
片方だけ入る場合もあるのですか? <<<TOP
あります。たとえば、磁場をかけた場合や、強磁性体では、片方だけ
入ります(だから、強磁性体になっているのです!)
それ以外では、大抵は、エネルギーがスピンに関して縮退していますから、
同確率で占有されます。あくまで確率が等しいのであって、必ずペアで
入っているという保証はありません。
たとえば、スピン1/2の場合(例えば電子)、全粒子数が奇数か偶数か
によって、最上位、すなわちフェルミ波数の準位に入る粒子が、一つ
(奇数の場合)か、二つ(偶数の場合)のケースが有り得ます。もし、最上位
の粒子数が1つだと、スピンの持つ磁性がキャンセルされず、残ること
になり、磁性に大きな違いが出ます。これは実際、直径数百Åの金属超
微粒子では、顕著に見られます。
でも、散らばっている確率がありましたが、これは絶対零度でも基底状態
にならない、ということですか? <<<TOP
違います。
まず、お尋ねの説明とは、「三つの状態に三つの粒子が入る場合」の
説明のことですね。
あれは、十分低温な場合、ということで、絶対零度ではありません。
絶対零度ではもちろん、全部基底状態に落ちます。
参考) 「統計力学入門」高橋・講談社、p262
高さ∞のポテンシャル井戸を考えた場合とで、違いはありますか? <<<TOP
大事な質問です。おっしゃるように、C を定数として、
周期的境界条件では、j (x)~exp(iC 2pn), n=0, ±1, ±2,...
井戸型ポテンシャルでは、j (x)~sin(iC pn), n=1, 2, 3,...
です。周期的境界条件の方が、波数の間隔が2倍になっていますが、
これは、nの負号が正負ありますから、結局、トータルでは同じ状態数
となります。
もう一つ、原点のゼロは、周期的境界条件の方にのみ現れますが、
これも、状態数としては「1つ」なので、エネルギーの原点をそこ(=零点振動
のエネルギー)に取れば同じことです。
ただ、井戸型ポテンシャルでは、波数が良い量子数にならない
(∵行ったり来たりしている定在波なので運動量の固有状態ではない)
ので、周期的境界条件で考えた方がわかりやすいと思います。
注) メモを見返すと、井戸型ポテンシャルで説明したときにもsin関数
の中身の係数を2pとしてしまっているようですね。次回、訂正することにします。
また、どういう場合に古典統計と一致するのですか? <<<TOP
これも大事な質問だと思います。
まず、古典理想気体の一粒子あたりの比熱は、密度や温度、圧力等に
よらず、C = kB/2 (1次元の場合)
でした。実は、レポートNo.1では、エネルギー準位間隔Dの値によらず、
中程度の温度域 ( D<< kBT << nmax2D / kBT )において、C ≒ kB/2 となる
のです。
一般に、比熱は「ある量」の物質の「温度」を変えたときに吸収・放出する「熱量」
と言う定義ですから、「ある量」、「温度」、「熱量」の単位によって、値が
変わります。ですから、
"単位系はいつでもSI"と言う新入生的考えは捨てて、臨機応変に単位を
変えて式を作り直してみることで、式の意味がわかりやすくなる場合があります。
たとえば、
「ある量」=1モル、1g、1cc、1粒子、etc.
「温度」=1K、1kBK、etc.
「熱量(エネルギー)」=1J、1dyne、1cal、etc.
などですが、今回のレポートの場合、「ある量」を1粒子、「温度の単位」を1kBK
「熱量の単位」を1Jにとると、判りやすいという話でした。
余談)他にもエネルギーの単位として、たとえば、E=mc2から、1(g×c2)を使う
などということも有り得ますし、1粒子の持つエネルギーに限定すれば、
磁場(mBH)、速さ(mv2/2)、波数(hbar2k2/2m)、波長(h2l-2/2m)、周波数(hn)、
角周波数(hbarw)、温度(kBT)、電圧(eV)などもエネルギーの単位として使えます。
どうして D=1 としてしまっているのですか? <<<TOP
こういう穴(悩み)に陥るケースは意外と多くあるものです。気が付いて
しまえば何と言うことはないのですが、、、。 スケール(scale)という大事な
概念も含んでいるので是非、慣れていただきたいと思います。
今の場合、一言で言えば、エネルギーの単位をDにしているということです。
(e / D を求めたのと同じ)
もちろん、エネルギーの表式は、
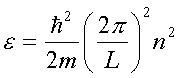
なので、プランク定数、フェルミオンの質量、円周率、箱の大きさなどの
量を含んでいますが、これらは全て定数ですからまとめてしまって、D=1
の場合について調べた、と思ってもOKです。
このように、式全体にかかっている定数をまとめてしまって、それを単位
にして計算することを、「スケールする」と言います。