2001統計力学II Q&A-9 (12/21回収分)
<<<戻る
注)読みやすいように文体を多少改変・統一してあります。
良問(?)には苗字を公開してありますが、困る人は申し出て下さい。
また、苦情や不満についてのコメントを公開する場合は必ず匿名としますので、
辛口のコメント もどしどしお願いします。
*できるだけ具体的に書いていただけると対応・補足できます。
例:「よくわからなかった」⇒「二重和の取り方で、なぜ束縛条件が外れるのかわからなかった」
Q's
- 相互作用のあるスピンの問題で、トレース(Tr)をとる時に、
Tr C-1HC =
Tr H
左辺のトレースが、「固有状態ではない基底ベクトル」でとるという点が
理解できなかった。(浜崎)<<<TOP
後藤 注) 上の式で、H
が対角化されているハミルトニアンとしています。
念のため。
- 多数のスピンが相互作用している問題で、三つ以上は解けないのでは?(石川)<<<TOP
- 格子比熱の問題で、デバイモデル以外の近似モデルはないのですか?(乙黒)<<<TOP
- 格子振動の最大振動数nmax≡nDの考え方(1)で、「隣接原子が逆に動く振動」
という意味がわかりません。(野村、戸田) <<<TOP
- 格子振動の最大振動数nmax≡nDの考え方(2)で、「独立な振動モード=3N
」
という条件の意味がわかりません。(黒田) <<<TOP
- 格子振動のところで、波長が短くなって行き、l=a
まで行くとl=0
と一緒、と
言われましたが、l=∞ ではありませんか?(梶田)<<<TOP
- 愚問かも知れませんが(原文ママ)、T→∞(高温)としたときの、高温とは
実際にはどれくらいの温度なのですか?実現できるのですか?(梶田)<<<TOP
- 格子振動の「モード」の意味がわかりません。(松井、三宅)<<<TOP
特に状態密度が、格子振動の場合=(3/2)×光子の場合
となる理由がわからない。
- 剛体球のポテンシャルとは何ですか?(久保)<<<TOP
- 格子比熱はなぜ、高温で一定になるのですか?(野村)
<<<TOP
- 学生実験で、電気抵抗の温度変化の要因は格子振動であり、電子による
散乱は殆ど効いていないと習いましたが、それと電子の比熱がフェルミ面
近傍の電子のみによることと関係ありますか?(藤波)<<<TOP
- ボースアインシュタイン凝縮の臨界温度を求める際に、別の教科書で、
Appel関数を用いていたのですが講義でやった方法と同じですか?(田中)<<<TOP
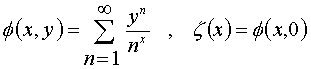
- ボースアインシュタイン凝縮の臨界温度を求める際に、下式の
和が定数になる理由がわかりません。(野村)<<<TOP
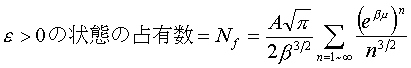
- (いくつかの球の連成振り子で)一つの球を端にあてると、反対側の球が
動くというおもちゃがありますが、その原理と音波が関係していると聞いた
ことがあります。これは固体中の格子振動のことでしょうか?(富沢)<<<TOP
| ||||| |
〇←…〇〇〇〇〇←〇
- スピン相互作用で、イジング型やハイゼンベルグ型のハミルトニアンは
どうやってもとめたのですか?(東)<<<TOP
- スピン相互作用のある系で、強磁性と反強磁性の磁化の磁場依存性の
違いの原因は何ですか?(梅田)<<<TOP
後藤 注)
原文には反磁性とありましたが、反強磁性と反磁性は異なる意味で、
ここでは反強磁性と直して置きます。
- N次元球の状態数の導出が未だに出来ません。(子長谷)<<<TOP
- スピンというのは粒子の自転みたいなものですか? それにしては↓と↑しか
状態がありえないというのは、、、(小野)<<<TOP
- スピン相互作用(イジング型)について。↑━↑という絵を書かれましたが、
二つのスピンの向きはどちらも上を向いているのですか?
(長田)<<<TOP
- 光子について考えるとき、スピンを考慮する必要があるのですか?(佐藤)<<<TOP
- 光子の性質で、粒子数不定からμ=
0を導くやりかたがわかりません。(増岡)<<<TOP
A's
- 相互作用のあるスピンの問題で、トレース(Tr)をとる時に、
Tr C -1HC
= Tr H
左辺のトレースが、「固有状態ではない基底ベクトル」でとるという点が
理解できなかった。(浜崎)<<<TOP
トレースは、線型代数で習ったように、行列の対角成分の和です。
一旦、N×Nの行列の形に書いてしまえば、どちらも、単に対角成分の和をとる
ということで変わりはありません。
しかし、ハミルトニアンは元々演算子です。よって、これをN×Nの行列の形に
書くためには、基底ベクトルを決めなければなりません。
左辺でC-1HC
の形に書いたということは暗黙の内に、基底ベクトルを
xからCxに変えているのです。
- 多数のスピンが相互作用している問題で、三つ以上は解けないのでは?(石川)<<<TOP
力学で、三体以上は、変数が9個あり、求められる「積分」である、エネルギー(スカラー値)、
運動量(ベクトル)、角運動量(ベクトル)の個数7つを超えてしまうので、解けない、という
風に教わったわけですね。
量子力学では三体どころか、二体でさえも厳密には解けない場合が多くあります。
水素原子は厳密に解けますが、水素「分子」ではすでに近似的にしか求まりません。
多数のスピンが相互作用している問題でも、一つ一つのスピンの動きの時間変化は
統計力学では全くわかりません。統計力学の目的は、そのような一つ一つのスピンの
ミクロな動きがわからなくとも、平均値をうまく計算してしまおう、というところにあります。
- 格子比熱の問題で、デバイモデル以外の近似モデルはないのですか?(乙黒)<<<TOP
イ ) 等分配則を無理矢理当てはめたのがC
=3NkB
のデュロンプティ則
ロ )
一つ一つの原子が古典的な調和振動子(動き回らない)として振る舞う
というモデルが、アインシュタインモデル(低温で指数関数的に減衰)。
などがあります。
- 格子振動の最大振動数nmax≡nDの考え方(1)で、「隣接原子が逆に動く振動」
という意味がわかりません。(野村、戸田) <<<TOP
下図のように、左右の隣同士が離れたりくっついたりする振動モードです。
○→ ←○ ○→ ←○ ○→ ←○
←○ ○→ ←○ ○→ ←○ ○→
○→ ←○ ○→ ←○ ○→ ←○
これが最大波数(最短波長)で、かつ最大周波数(最短周期)の振動です。
解析力学の「バネでつながれた多数の質点の振動」を思い出して下さい。
- 格子振動の最大振動数nmax≡nDの考え方(2)で、「独立な振動モード=3N
」
という条件の意味がわかりません。(黒田) <<<TOP
三次元のN個の粒子の運動は、3N個の成分のベクトルで表されることを
思い出して下さい。格子振動は、バネでつながれた質点の振動と思って
良いので、この基準振動を行列の対角化で求めれば3N個の基準振動
が求まります。これを指して、「独立な振動モード」と呼んでいます。
- 格子振動のところで、波長が短くなっていき、l=a
まで行くとl=0
と一緒、と
言われましたが、l=∞ ではありませんか?(梶田)<<<TOP
そのとおりでした。k =0と混乱していました。
- 愚問かも知れませんが(原文ママ)、T→∞(高温)としたときの、高温とは
実際にはどれくらいの温度なのですか?実現できるのですか?(梶田)<<<TOP
大変良い質問です。温度が非常に高いとか、低いとか言うのは、絶対的なもの
ではなく、必ず、何かと比べた場合の話です。
例えば、自由電子の比熱であればフェルミ温度と比べるし、格子比熱であれば、
デバイ温度と比べることになります。
他の場合でも、出てきた式の次元を調べると、T/[温度の次元を持つ何かの量]
という形になっていると思います。
もう一つの質問で、∞の温度を実現できるかということですが、格子系の
温度を上げてしまうと、みんな解けて蒸発してしまいますが、特定の部分系
(たとえば、原子核スピンのスピン温度)の温度を∞にしたり、あまつさえ、負にした
りすることも可能です。
- 格子振動の「モード」の意味がわかりません。(松井、三宅)<<<TOP
特に状態密度が、格子振動の場合=(3/2)×光子の場合
となる理由がわからない。
これまで、状態を指定するのに波数やエネルギーを使ってきましたが、
波数やエネルギーだけでは状態を一つに絞りきれない場合があります。
電子のスピンや、格子振動の縦波・横波、光子の偏波方向、etc.
などです。これらを総称して「モード」と言います。
ただ、スピンや偏波方向は、その単語の方がわかりやすいので、
わざわざモードと言い換えることはしません。
格子振動は3つのモード(縦波、水平偏波の横波、鉛直偏波の縦波)
があり、光子は、二つ(水平偏波の横波、鉛直偏波の縦波)だけですから、
比を取ると、3/2が出ます。
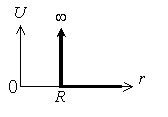
- 剛体球のポテンシャルとは何ですか?(久保)<<<TOP
剛体球の半径をRとすれば、下図のようなポテンシャルです。ようするに、
半径内には絶対に入れない、という非常に単純なことです。
- 格子比熱はなぜ、高温で一定になるのですか?(野村)
<<<TOP
線形独立な振動の数が3N個しか無く、これに熱エネルギーが等分配
されるためです。
- 学生実験で、電気抵抗の温度変化の要因は格子振動であり、電子による
散乱は殆ど効いていないと習いましたが、それと電子の比熱がフェルミ面
近傍の電子のみによることと関係ありますか?(藤波)<<<TOP
パウリ排他律のために電子−電子散乱は起こりにくくなっているという
意味ではその通りです。
- ボースアインシュタイン凝縮の臨界温度を求める際に、別の教科書で、
Appel関数を用いていたのですが講義でやった方法と同じですか?(田中)<<<TOP
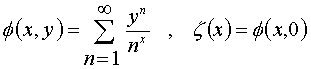
全く、同じです。単に関数に名前(Appel)をつけているだけです。それほど
メジャーな関数でない(⇔ツェータ関数はメジャー)のと、名前を出しても
ご利益がないので講義では触れませんでした。
- ボースアインシュタイン凝縮の臨界温度を求める際に、下式の
和が定数になる理由がわかりません。(野村)<<<TOP
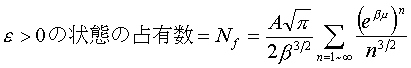
低温では粒子数を一定に保つために、化学ポテンシャルが負の値から
どんどんゼロに近づいて行きます(ゼロを超えることは絶対にありません)。
よって、限りなくゼロに近づいた状態では、和の分子は1ですから、βに
依存しなくなり、定数となるのです。
- (いくつかの球の連成振り子で)一つの球を端にあてると、反対側の球が
動くというおもちゃがありますが、その原理と音波が関係していると聞いた
ことがあります。これは固体中の格子振動のことでしょうか?(富沢)<<<TOP
| ||||| |
〇←…〇〇〇〇〇←〇
片端に球を当てると、繋がった球から球へ、ソリトン的(孤立波)な
弾性波が伝わっていって、反対の端で、最後の球に衝突し、一つだけ
突き飛ばされるというイメージですが、伝わるのはあくまでソリトン
なので、格子振動とはちょっと違うと思います。
- スピン相互作用で、イジング型やハイゼンベルグ型のハミルトニアンは
どうやってもとめたのですか?(東)<<<TOP
量子力学か、固体物理、物理実験学(磁気共鳴)などの講義でやります。
ハイゼンベルグ型は、要するに、同じ向きのスピンはパウリ排他律で近寄
れないので、クーロンエネルギーは低くなって安定、ということから求められます。
以前の数理物理演習III(量子力学)の問題11をどうぞ。
イジングは、これに、電子の軌道角運動量を組み合わせて、スピンが
特定の方向しか向けないということを考慮すると出てきます。
- スピン相互作用のある系で、強磁性と反強磁性の磁化の磁場依存性の
違いの原因は何ですか?(梅田)<<<TOP
後藤 注)
原文には反磁性とありましたが、反強磁性と反磁性は異なる意味で、
ここでは反強磁性と直して置きます。
それほど面倒なことではありません。
かけた磁場が弱い場合は、隣のスピンとの相互作用でスピンの方向が
決まっています(強磁性なら同じ向きに揃っているし反強磁性なら、
逆向きに揃う)。
しかし、磁場が強くなると、どちらもその磁場の向きに揃うようになります。
これを「スピンフロップ現象」と呼ばれます。
強磁性 反強磁性
低磁場 ↑↑ ↓↑
高磁場 ↑↑ ↑↑
注)磁気異方性がある場合は、磁場をかける方向がスピンに平行か
垂直かで、もっと奇妙なことが色々おきます。詳しくは固体物理IIで。
- N次元球の状態数の導出が未だに出来ません。(子長谷)<<<TOP
周期境界条件を課すると、特定の波数を持った状態しか存在しない、という
ところがポイントです。
状態密度の簡単な覚え方としては、dkN/(2p)N
から kN→
e への変数変換で
出すという方法もあります。講義ノートを参照してください。
- スピンというのは粒子の自転みたいなものですか? それにしては↓と↑しか
状態がありえないというのは、、、(小野)<<<TOP
もちろん、スピンは磁場に対して、斜めでも横でもいろんな方向を取り得ます。
よく、1/2のスピンはup, downの二通りの状態しか無い、と言われるのは、
ハミルトニアンH=aIZ
(aは定数)の固有状態(≡時間が経過しても不変な状態)
が二つしかかないということです。この |↑> と |↓>
の線形結合で、任意
の方向(θ,φ)を向いたスピンの状態を表すことが出来ます。
- スピン相互作用(イジング型)について。↑━↑という絵を書かれましたが、
二つのスピンの向きはどちらも上を向いているのですか?
(長田)<<<TOP
いいえ違います。単に、二つのスピンが相互作用している、という絵を
描いただけで、実際のスピンの向きは色々あります。(その平均を出そう、
というのが統計力学の目的です)。
- 光子について考えるとき、スピンを考慮する必要があるのですか?(佐藤)<<<TOP
まず、振動の偏波方向が、光子のスピンに対応していますので、エネルギー
や比熱を求める際には偏波方向のモード数2を考慮すればスピンを考慮した
ことになります。
- 光子の性質で、粒子数不定からμ=
0を導くやりかたがわかりません。(増岡)<<<TOP
カノニカルで粒子数一定の条件を外して、色々な粒子数で全部和を取ると、
グランドカノニカルのμ= 0の表式が出てきます。
<<<戻る