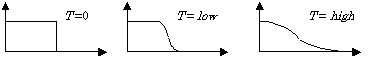2001統計力学II
Q&A-2 (10/12)
<<<戻る
注)読みやすいように文体を多少改変・統一してあります。
良問(?)には苗字を公開してありますが、困る人は申し出て下さい。
また、苦情や不満についてのコメントを公開する場合は必ず匿名としますので、
辛口のコメント もどしどしお願いします。
*できるだけ具体的に書いていただけると対応・補足できます。
例:「よくわからなかった」⇒「二重和の取り方で、なぜ束縛条件が外れるのかわからなかった」
Q's
A's
- Fermi粒子とBose粒子のちょうど、間の性質を持つような粒子、すなわち、
一つの状態に3つとか4つしか入れない、というものはないの? <<<TOP
非常に良い質問です。数十年前に、パラ統計として、さかんに最先端の研究
が行われたことがあります。
残念ながら、現実の粒子ではそういうものは存在しないのと、パラ粒子は、
結局、「複数のフェルミ粒子を組み合わせたもの」、という風に捉えることが
出来るので、最近はあまり、流行らないみたいです。
日本物理学会誌(和文の雑誌)の23巻, p644-653(1968年9月号)
に解説記事が載っているそうです。私は未だ読んだことはないのですが。
- 板書で、Slater行列式の規格化因子が
1/(√N)
になっていた。
(正しくはもちろん、1/(√N
!)
です)
指摘、ありがとう、書き忘れていたようです。来週、訂正します。 <<<TOP
- Bose分布の分布関数<ni>が負になってしまいそうなのですが、、、。 <<<TOP
nは粒子数ですから、絶対に負にはなりません。そこで、μ≦
0 という
条件が直ちに出てくるのです。
- グランドカノニカルでの二重和の取り方がピンと来ませんでした
<<<TOP
簡単のため、Fermionの例を図示すると、、、
(Bosonの場合は、n0=0, 1,
2,... ですのでもっと多くの場合があります)
A) 粒子数N 毎に和を取って行くやり方の例(二重和の方です)
n0 , n1
, n2 , n3 , n4
N = 0の場合
1) 0
0 0
0 0 ...
N = 1の場合
1) 1
0 0
0 0 ...
2)
0 1
0 0 0 ...
3)
0 0
1 0 0 ...
4) 0
0 0
1 0 ...
:
N = 2の場合
1) 1 1
0 0 0 ...
2) 1 0
1 0 0 ...
3) 0 1
1 0 0 ...
4) 1 0
0 1 0 ...
5) 0 1
0 1 0 ...
6) 0 0
1 1 0 ...
:
B)
各エネルギー準位について無条件に和を取るやり方の例
1) 0 0
0 0 0 ...
2) 1 0
0 0 0 ...
3) 0 1
0 0 0 ...
4) 1 1
0 0 0 ...
5) 0 0
1 0 0 ...
6) 1 0
1 0 0 ...
7) 0 1
1 0 0 ...
8) 1 1
1 0 0 ...
9) 0 0
0 1 0 ...
:
この二つのやり方A), B)が、結局どちらも同じということです。
(粒子数毎にわけても、結局、全部の場合について和をとるので)。
- 占有数ni の意味がよくわからなかった。そもそも
「 eiの占有数」とは何?
フェルミ粒子だと、同じ状態に一つしか入れないから、ni
= 0,1 で、
ボース粒子だと、いくつ入ってもいいから、ei
= 0,1,2... でよいのですか? <<<TOP
量子力学で、一つの粒子に関する問題を解いてエネルギー準位を求めます。
e0 , e1
, e2 , e3
, e4 , e5
,.....
この段階では、あくまで一つの粒子に関する問題で、温度とか、エントロピーとか
は全く判りません。
次に、その粒子が沢山集まったときに、どういう状態になるか、というのを統計力学
でやります。このとき、たとえば、
e3 のエネルギーを持っている粒子の数が、e3の占有数です。
後半の質問は、それで正しいと思います。
- 講義終了直前に板書のスピードを上げないで欲しい。
とても書ききれない。
<<<TOP
大変的を得た、良い忠告です。ありがとう。ついつい、間に合わないと急いで
書いてしまうことがありますが、本講義の次の時限の講義もあるので、数分
前には書き終わるようにしたいと思います。
- たとえ話がわかりやすくてよい。もっとたとえ話を引用して欲しい
<<<TOP
イメージがつかめないと、いくら式の計算が出来てもなかなか前に進めない
ので、できるだけたとえを引用したいと思っています。
但し、残念ながら「化学ポテンシャル=講義のつまら無さ」というたとえは、
私のオリジナルではなく、統計力学入門(講談社、高橋康)の受け売りです。
- Fermionの分布関数のグラフを、β=∞(T=0), β=小(T=低温),
β=中(T=高温)
と、三つでまとめてしまうのは良くないと思います(横軸の関係) <<<TOP
コメントの意味がちょっとつかめないのですが、大事なことを言っている気がするので
ぜひ、もう少し詳しく伝えて下さい。
私の予想では、可能性として、
1)
化学ポテンシャルが温度変化するので、横軸を揃えてプロットするのは良くない。
2)
フェルミ分布関数は温度によって連続的に変化するから、3つだけを代表例として
しまうのは不十分である。
のどちらかかな、と思っています。もし、1ならば、次回、じっくりと、化学ポテンシャルの
温度変化を議論します。もし、2ならば、是非、自分で、グラフを書いて、温度とともに
フェルミ分布関数が、美しくうねるようすを堪能して下さい。
- Fermi分布関数が高温で「なまる」理由の物理的描像は何でしょうか。
粒子が振動するからですか? <<<TOP
「振動」という意味を「熱振動」つまり「運動エネルギーが大きくなり、ランダムに激しく
動く」という風に理解していらっしゃるのであれば正解です。
きっちり全員着席している教室で、後ろのドアの近くで、面白い漫才をやっていると、
みんな浮かれ出して(≡教室の温度が上がって)、ドア付近に座っていた人達から、
少しずつ出て行ってしまう、、、、ということです。
- Slater行列式で、Bosonに対応した方(添字で+を付けた方)の具体的な
計算を示して欲しい。
<<<TOP
2×2の行列ならば、ad+bc です。
- Fermionについて、例えば、s軌道に二つ電子が入った後でも、空間的には
まだまだスペースがあるように思えるのですが、どうしてそれ以上入れないのか
物理的な描像を示して欲しい。何か斥力が働いているとは考えにくいですし、
何がこれ以上電子が入ってくるのを妨げるのでしょうか。 <<<TOP
大変良い質問です。「斥力のようなもの」が働いていると思ってよいのです。
教科書によっては、この仮想的なポテンシャルがどんな形か計算させて
いるものもあります(グライナーの統計力学など)。
ただ、あくまで「斥力のようなもの」でして、本当のポテンシャルではありません。
なお、Bosonでは逆に、「引力のようなもの」が働いています。
- 量子力学、統計力学と混ざっていて、いよいよ現代物理だ、と思いました。
<<<TOP
確かにそうですが、まだ、やっと19世紀の物理学です。3年生の1年間で
一気に、100年の時空を通過し、卒研と大学院での最先端の研究に入ります。
上手に「ワープ」できるよう、お手伝いできると良いのですが、、、。
- グラフを描けない。 <<<TOP
意外と簡単です。Excelでは、x軸とy軸のデータを指定して、「散布図」というグラフを
選びます。そのほか、sma4winというグラフ描画ソフトが関数描画機能を持っていて
使いやすいと思います。コンピュータルームのTAに聞いてみるのが良いでしょう。
<<<戻る
<<<TOP