の解をどうして、波の形
第三回コメント回答 <<<戻る
webの感想を述べよということでしたが、概してポジティブなものが多かったです。
記名提出の感想ですから、額面通り受け取れないとは思いますが、多少なりとも
役に立てば幸いです。
具体的な感想・質問に対する回答を以下に示します。
2)
座標変換のやり方は決まっているのかそれとも、その都度自分で
考えるのか。
3) 変分法のコメント(第一回A2)で、f(x)の一次微分がゼロだと、
どうして二次の項が効いてくるのか。
4) リング状に多くの質点が並んだ系で、運動方程式
![]()
の解をどうして、波の形
![]() に仮定したのか。
に仮定したのか。
5)
振動の問題で、固有振動数と同じ振動数の外力がかかると、
どうしてエネルギーが供給されつづけるのか(第二回コメントQ-9)。
6)
真空中を伝わる電波は線形であるとのことだが、非線形な振動には、
どのようなものがあるか。
8) 質問が出席票に書ききれない⇒もちろん、メールや直談判でどうぞ。
9)
生徒の質問に対する回答がためになった⇒大学生は生徒ではありません。
(文部科学省の定義:
小学生=児童、中高生=生徒、大学生=学生)
10) 出席・レポート・ノートテーク状況に関する配点は?(同様の質問多数)
回答
昨年度の問題の略解を載せて置きます。しかし、解答が掲載された
問題は試験には出題されない確率が高い(ゼロではない)ことを承知して下さい。
なお、上級生(特に大学院生)に噛み付いて、答を聞き出すのは、
物理の勉強の非常に大事な訓練の一つです。
2)
座標変換のやり方は決まっているのかそれとも、その都度自分で
考えるのか。 <<<TOP
もちろん、その都度、考えます。丸っこい系が出てきたら極座標、
四角い箱なら、デカルト座標、コロッケ型なら楕円座標、複数質点なら
ウマい基準座標を、、、くらいの方針しか知りません。もし、誰も知らない
座標変換を発明できたら、物理学史に名前が残ります。
3)
変分法で、f(x)の一次微分がゼロだと、どうして二次の項が効いて
くるのか。(第一回コメントA2) <<<TOP
もちろん、ゼロでなくとも、二次の項は多少効いています。しかし、
f(x)を滑らかな関数(つまり、f'(x)やf”(x)の大きさが極端に
大きかったり小さかったりしないということです。この仮定が大事)
とすると、
f(x+dx)=f(x) + f'(x)・dx + f”(x)・(dx)2/2
にたとえば、dx=0.001
を代入してみれば、(dx)2の項は、10-6
程度と、非常に小さくなることがわかります。ですから、二乗の項は
存在はしているんだけれど、f(x)や、f'(x)・dx
の項に比べて極端に
小さいので無視できるのです。
これに対し、もし、 f'(x)が完全にゼロだと、dxが先ほどと同じ
大きさなら無視せざるをえませんが、もう少し大きくなって0.1くらいに
なると、(dx)2/2=0.005ですから無視出来なくなりますよ、という
わけです。
4)
リング状に多くの質点が並んだ系で、運動方程式
![]()
の解をどうして、波の形
![]() に仮定したのか。 <<<TOP
に仮定したのか。 <<<TOP
バネで繋がれた質点だから、おそらく波のように振動するだろう、という
直感です。単なる式変形ではなく、こういう「直感」も物理には必要です。
しかし、物理では単なる直感ではもちろん、ダメで、そう仮定したら、代入して
成り立つことを確かめる必要があります。
(もちろん、純粋に数学的に解を求める方法もありますが非常に大変です)。
5)
振動の問題で、固有振動数と同じ振動数の外力がかかると、
どうしてエネルギーが供給されつづけるのか(第二回コメントQ-9)。 <<<TOP
大変良い質問です。答は単純で、
![]() を解くだけです。
を解くだけです。
すると、解に、時間に比例する項が現れます。是非、チャレンジを。
(ヒント─右辺=0の一般解は ![]() です。右辺を含めた特解を
です。右辺を含めた特解を
![]()
と置いて代入してGを求めればよいのです。)
6)
真空中を伝わる電波は線形であるとのことだが、非線形な振動には、
どのようなものがあるか。 <<<TOP
空気や水をはじめとして、物質(波が伝わる物質のことを媒質と言います)の中を
伝わる場合はほとんど非線形です。ただ、空気などは、その非線形の度合いが
非常に小さいので、殆ど線形とみなしてよいのです(真空と同じと考えてよい)。
物質の中を波が伝わるとき、にどうして非線形になってしまうかというと、
伝わる波の影響で、物質の状態が変化(≡分極)するからです。この分極の
大きさが、波の振幅に比例していれば、線形なのですが、二乗や三乗の項が
入ってくると、非線形となります。
ガリレイ変換(t'=t, x'=x-vt)ではなく、ローレンツ変換
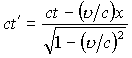
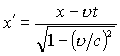
が必要になり、運動している物体の長さや時間、質量が変化します。
エネルギーは、
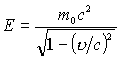 、質量は、
、質量は、
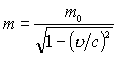
そして、ラグランジアンは、
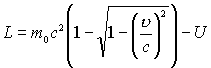 という形になります。
という形になります。
ポテンシャルも、座標だけに依存するもの(バネのポテンシャル)などは、
あり得ない(ローレンツ収縮のために、速さに応じて長さが変化するため)、
「剛体」というもの自体が存在しない(「力」が瞬時に先端まで伝わることがあり
得ないため)、など、いろいろな「こと」が起こってきます。
ぜひ、量子力学・統計力学と合わせて勉強して下さい。
基本的に出席ゼロでも減点はしませんので、試験で及第点を取る自身のある人は、
講義に出なくともOKです。つまり、試験でAの点数を取った人は必ずAです。
試験で惜しくも及第点を取れなかった人に限り、出席・ノートテーク・レポートが良好だと、
及第限界点(≡C評定)まで持ち上げる可能性があるというのがポリシーです。